Compressing calldata - L2 fees cut by 50%

TL;DR:

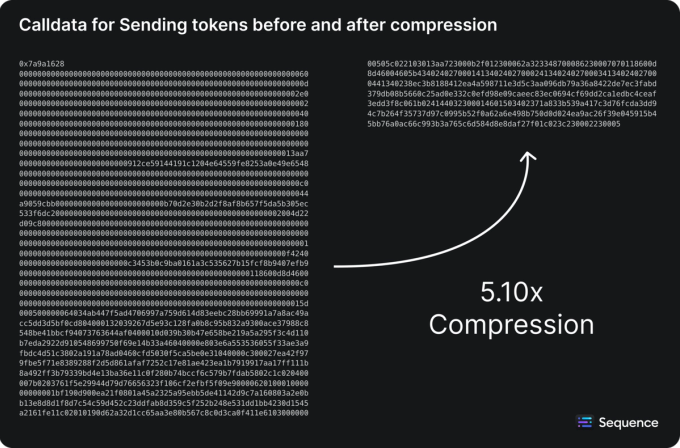
We have reduced gas costs on L2s by ~50% for all Sequence transactions. We have achieved this by compressing calldata by ~5x. These savings automatically impact all wallets without the users having to update them. The compression is now live on Arbitrum, Arbitrum Nova, Optimism, and Base.

In the EVM chain ecosystem, there are primarily two kinds of networks: L1s and L2s. L1s are standalone chains that don't need to primarily hook to another chain to work. In this category, we find chains like Ethereum.

The other category is L2s. These chains use a combination of techniques to leverage the properties of an underlying L1, allowing L2 chains to relax their operational limits and thus reach higher throughput.

We will focus specifically on one kind of L2, the rollup. Here, we can find networks like Arbitrum, Optimism, Polygon zkEvm, base and zkSync.

Rollups work by an amalgamation of two properties:

• All "input data" is published, allowing anyone to read it.

• Anyone can "raise an alarm" if they see that the blockchain does something it shouldn't do.

This is (again) a big simplification, but the important thing is that a rollup operates with a different set of trust assumptions.

In a rollup, anyone can read the data, and anyone can verify it (so far, like an L1), but the difference is that if one entity sees something wrong, it can alert all other entities. This means that the network can be safe as long as there is one honest participant in the whole network.

How Does This Relate to Calldata?

In an L1, a majority of the nodes need to be able to sync and validate the chain. However, in a rollup, as long as one honest entity is able to validate, then the chain is considered safe. This allows the rollup to increase the "requirements" for running a node, without compromising on decentralization.

But there is still a "hard" requirement:

All "input data" is published, and anyone can read it.

This means that, even if the rollup can afford to make running a node expensive, it still needs to deal with publishing all this data. Rollups publish this data to a data availability layer (like an L1 or Celestia), leveraging the properties of the L1 to ensure that the data is available for everyone.

This leads to an interesting property: both Rollups and L1s have gas, but they price certain actions differently.

L1 Networks tend to charge more for computation and "long-term storage," since every node must replicate these values for the network to be secure.

L2 Rollups, on the other hand, charge a lot less for computation and storage, but they do need to charge more for input data (calldata) as this needs to be published into the L1.

Building a cross chain wallet

For most applications, this distinction is not a problem. If you are targeting L1s, you can use "stateless" patterns that move most data to calldata and only use the minimum required storage. If you are targeting a rollup, you can flip it around and move most data to storage, minimizing calldata.

But when building a cross-chain wallet, one of the desired properties is that the wallet must have the same address on different networks. This reduces the risk of the user sending funds to an "invalid address" on the wrong chain.

The problem is that, to get the same address on different chains, the initial code of the wallet contracts must be identical. There are ways around it (like starting all contracts with the same code and then doing chain-specific updates), but having the same contract implementation on all networks helps in different ways too, like simplifying the wallet architecture.

So, a wallet must choose: does it optimize for L1s or L2s? In Sequence, we optimized our wallets for L1s, meaning that almost all data is passed as calldata. This makes our wallet the cheapest AA wallet on L1s, but it has the side effect of increasing costs on L2s.

However, by implementing the following, we are releasing an update to our relayer, bringing down gas costs for L2s too.

Compressing data

One technique that allows us to achieve the best of both worlds is data compression. We can add an optional contract layer that decompresses the data, only to be later passed to the wallet contracts.

Let's go over a simple example of sending a transaction bundle, which does two things:

• It sends some ERC20 tokens.

• It sends some ETH payment to the relayer to cover the gas fee.

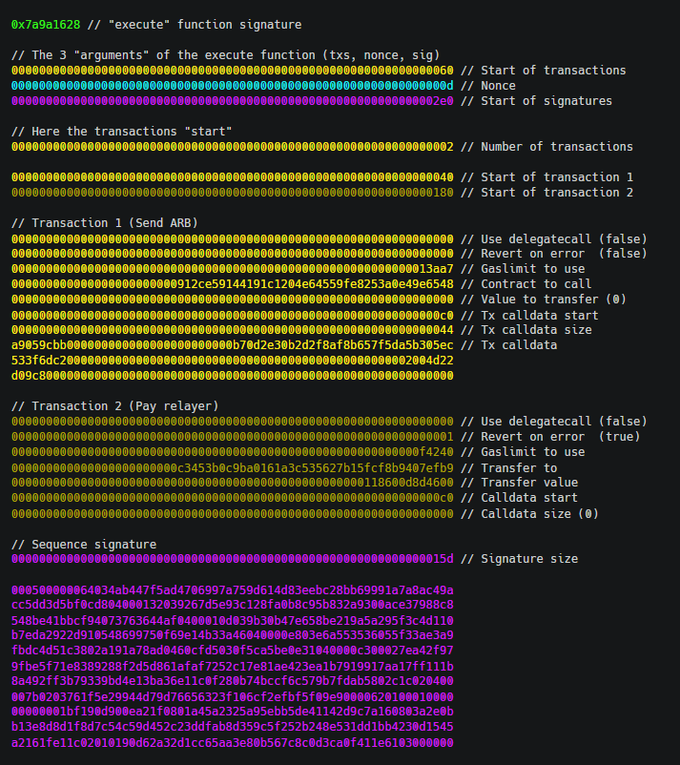
If we take a look at the decompressed calldata, we are going to see something like this:

0x7a9a1628
0000000000000000000000000000000000000000000000000000000000000060
000000000000000000000000000000000000000000000000000000000000000d
00000000000000000000000000000000000000000000000000000000000002e0
0000000000000000000000000000000000000000000000000000000000000002
0000000000000000000000000000000000000000000000000000000000000040
0000000000000000000000000000000000000000000000000000000000000180
0000000000000000000000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000000000000013aa7
000000000000000000000000912ce59144191c1204e64559fe8253a0e49e6548
0000000000000000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000000000c0
0000000000000000000000000000000000000000000000000000000000000044
a9059cbb000000000000000000000000b70d2e30b2d2f8af8b657f5da5b305ec
533f6dc200000000000000000000000000000000000000000000000002004d22
d09c800000000000000000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000000000000000001
00000000000000000000000000000000000000000000000000000000000f4240
000000000000000000000000c3453b0c9ba0161a3c535627b15fcf8b9407efb9
000000000000000000000000000000000000000000000000000118600d8d4600
00000000000000000000000000000000000000000000000000000000000000c0
0000000000000000000000000000000000000000000000000000000000000000
000000000000000000000000000000000000000000000000000000000000015d
000500000064034ab447f5ad4706997a759d614d83eebc28bb69991a7a8ac49a
cc5dd3d5bf0cd804000132039267d5e93c128fa0b8c95b832a9300ace37988c8
548be41bbcf94073763644af0400010d039b30b47e658be219a5a295f3c4d110
b7eda2922d910548699750f69e14b33a46040000e803e6a553536055f33ae3a9
fbdc4d51c3802a191a78ad0460cfd5030f5ca5be0e31040000c300027ea42f97
9fbe5f71e8389288f2d5d861afaf7252c17e81ae423ea1b7919917aa17ff111b
8a492ff3b79339bd4e13ba36e11c0f280b74bccf6c579b7fdab5802c1c020400
007b0203761f5e29944d79d76656323f106cf2efbf5f09e90000620100010000
00000001bf190d900ea21f0801a45a2325a95ebb5de41142d9c7a160803a2e0b
b13e8d8d1f8d7c54c59d452c23ddfab8d359c5f252b248e531dd1bb4230d1545
a2161fe11c02010190d62a32d1cc65aa3e80b567c8c0d3ca0f411e6103000000

This calldata contains:

• The nonce of the transaction (for replay protection).

• The list of transactions that we want to do (send ARB, send ETH).

• The signature for the smart contract wallet.

Let's disassemble it a bit further so we can understand each part:

In the disassembled image, we can better appreciate the different parts of the transaction, and we can spot different inefficiencies:

Static values

There are quite a few values that are always the same for all Sequence transactions. These include:

• The 0x7a9a1628 execute function signature.

• The "start of transactions."

• The structure of the transaction.

The structure of the transaction is the most important one, as lots of values (start of transaction, start of calldata, etc.) exist only to define this transaction structure. If we are going to build a compression schema that is only meant for Sequence transactions, then we can skip all this data.

Padded values

In multiple cases, we can see that we want to provide very little information (a boolean, a 2-digit number, etc.) but we still need to add a lot of zeros to their left.

This is because ABI encoding uses 32-byte words, so all values must be passed as 32-byte words. This leads to lots of wasted space in "0s"; we don't need 32 bytes to store "the number of transactions", we can just use 1 byte for that.

Bitmaps

We can go even further by using bitmaps to pass some data, for example, "revert on error" and "uses delegatecall" can only be true or false; we only need a single bit to express this information.

We can have a single "flags bitmap" per transaction. We can use the bitmap to express the following:

• Does it use delegatecall?

• Does it revert on error?

• Does it have a capped gas limit?

• Does it send a value?

• Does it have calldata?

This allows us to compress transactions significantly since when a transaction does not use a value, we can just not pass it; we don't even need to pass a zero.

A Few More Tricks

Function Selector

We can go a bit further by exploiting common patterns that appear in most transactions. For example:

0xa9059cbb is the function selector for sending ERC20 tokens. Sending ERC20 tokens is one of the most common actions on Ethereum, and it goes beyond just this example.

If we take the top 255 most used function signatures, we will see that they represent 90% of all Ethereum transactions. This means that for 90% of Ethereum transactions, we can represent their function selector with a single byte.

Scientific Notation

We can use scientific notation to represent "common numbers" in a more compact way. For example, most users always send amounts that are round numbers based on 10.

Let's say that you want to send 301.22 ARB. This might seem like a small number, but you must remember that ERC20 tokens tend to have 18 decimals.

When we include all the decimals, and we convert 301.22 ARB to binary, we get this:

0001 0000 0101 0100 0100 0100 0110 1010 0001
0001 0110 1011 0010 1010 0000 0000 0000 0000

We need 18 bytes to represent this small number! However, we can use scientific notation to represent it in a different way, using an exponent and a mantissa.

1016×30122=301220000000000000000

This alternative in binary can be represented as:

([constant 1010] ^ 01 0010) * 00 0111 0101 1010 1010

This lets us represent the exact same number, but using only 3 bytes. "Rounder" numbers can even get down to 2 bytes.

First Compression Pass

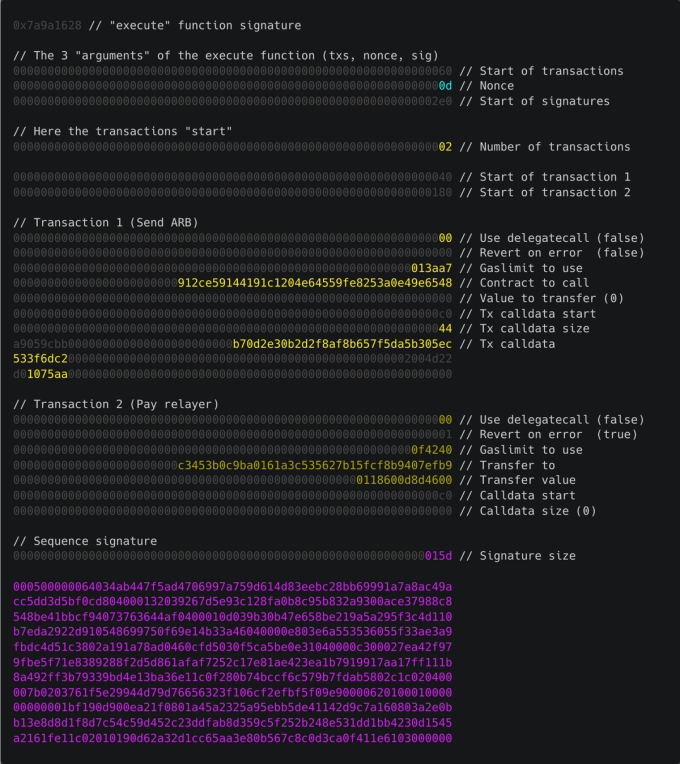
Let's see how much of the calldata we can trim away if we remove this redundant information:

The grayed-out text represents data that, after compression, we no longer need to include.

Of course, if we tried to compress the transaction down to only this data, we would be stuck with only being able to compress this very specific transaction. So, in real life, we need to add 1 extra byte before each colored part.

This strategy alone already gives us significant calldata savings, and so far, we are only compressing and packing; we are still relying 100% on calldata to pass around the information.

Obligatory Disclaimer

This post is not meant to be a critique of Solidity ABI encoding. ABI encoding has all this overhead because it must be cheap to read and cheap to write. Our compressed data will be unpacked in a single pass, and it is a lot harder to "write".

In other words, all this overhead exists because Solidity ABI can't specialize in a single task; it must work for all sorts of contract communication. In our case, we can specialize, and that's okay.

Second Compression Pass

So far, we've only tried to compress the data with the tools at our disposal (another calldata and code), but in rollups, it makes sense to use another tool for the job: contract storage.

In our example transaction, we have a few contract addresses, each one of them uses 20 bytes of calldata:

• 0x912ce59144191c1204e64559fe8253a0e49e6548 ARB token address

• 0xb70d2e30b2d2f8af8b657f5da5b305ec533f6dc2 ARB recipient

• 0xc3453b0c9ba0161a3c535627b15fcf8b9407efb9 Relayer address

The very first time we use these addresses, we must pass them as calldata, but we can take the opportunity to also store them in a sort of "directory". The next time any of these addresses need to be used, we can reference them by a "directory index" of only 3 bytes.

This lets us go from 60 bytes for 3 addresses to only 9 bytes total. Sequence Signature

I have avoided talking about the Sequence signature (the purple part) so far. The reason is that our signatures are already tightly packed, so we can't pack them much further.

However, our signatures are always proofs of a Merkle tree, so they do contain a lot of data that repeats from transaction to transaction.

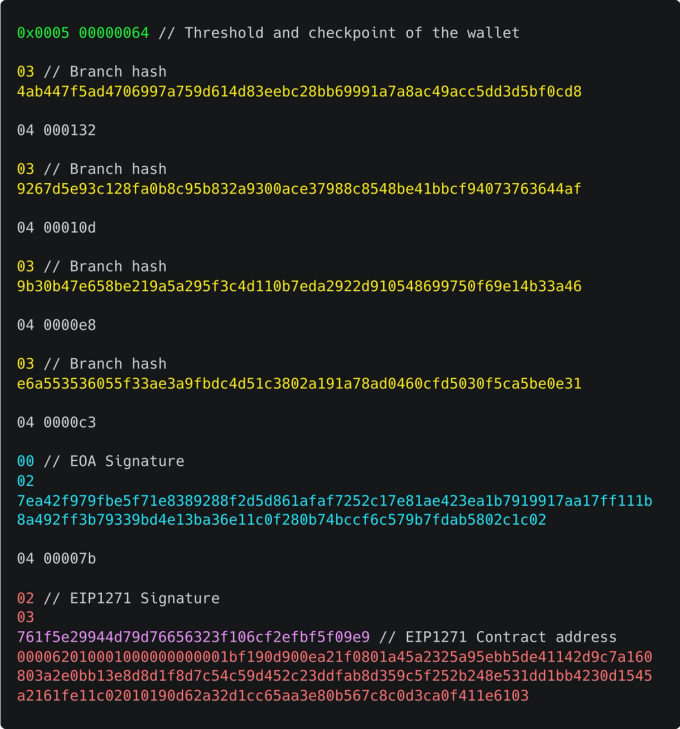
Let's analyze the example signature:

It is important to notice that most Sequence transactions have two inner ECDSA signatures, one wrapped inside an EIP1271 signature. So, this example signature contains:

• A Merkle proof.

• An ECDSA signature.

• An ECDSA signature wrapped inside an EIP1271, plus its own proof.

And the representation is still quite compact, but we can do better for L2s.

Branch Hashes

This signature is part of a tree, meaning the signature itself is a Merkle proof. When building the signature, we don't need to pass the contents of the whole tree, but we do need to pass the hashes of every unused branch.

This signature has a lot of branches! The reason is that this Sequence multisig wallet has >100 signers. This is not normal for Sequence, but it showcases how our transactions remain cheap even under heavy synthetic scenarios.

However, a key point is: branch hashes remain static across transactions (for a time, until the user rotates some keys). This means we can store them and reference them using indexes, just as we do with addresses.

Each branch hash takes 32 bytes. We can reduce them to only 3 bytes each.

ECDSA Signature

Sadly, EOA signatures can't be compressed (unless signature aggregation is used). For now, we will leave this data as-is.

EIP1271 Signature

In the case of EIP1271, one low-hanging fruit is to save the signer's wallet address to storage (like any other address), which gives us 17 bytes of savings.

Additionally, in this case, the EIP1271 signature is another Sequence signature. This means we can repeat the whole process again, compressing the inner EIP1271 signature too.

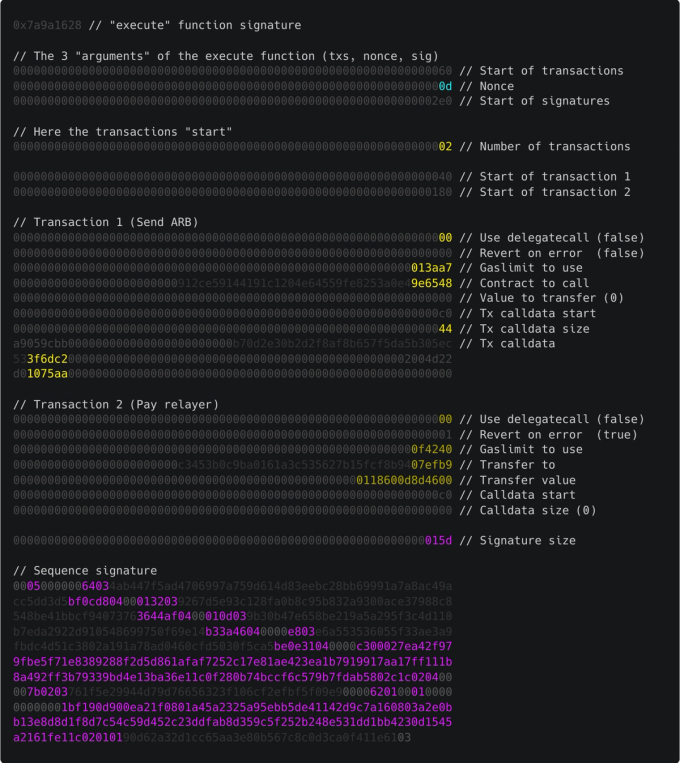
Final Trimmed Transaction

As I said before, this is only an approximation of the real compressed transaction; there is a bit more data that needs to be included.

However, we can appreciate how the whole transaction can be made more compact, not only the transaction data itself but also the signature.

Back to the Real World

We have implemented the above-mentioned compression schema for our Sequence wallets. It works using a custom-made state machine, implemented in Huff. This allows us to decompress the transactions in the most efficient way possible while retaining the flexibility of compressing any sort of transaction.

The above-mentioned transaction (a copy of it) can be compressed down to this calldata:

The original data goes down from 1124 bytes to 220 bytes, a compression ratio of 5.109. All this considering that the original data has 132 bytes of uncompressible information (the ECDSA signatures).

Show Me the Numbers

We tested a variety of compressed transactions on Arbitrum. It has to be mentioned that the same compression gains can be applied to Optimism-based networks. Arbitrum Nova also partially benefits from compression, but only from packing.

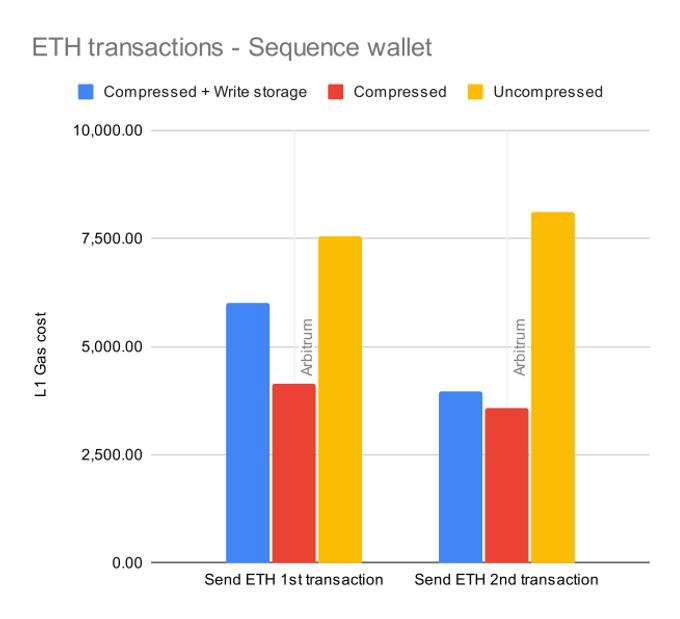
Sending ETH

This is the simplest scenario there is: sending ETH without doing anything more. In the example we perform this test twice.

In the first transaction, we need to write a lot of storage data (branch hashes, wallet address, etc.), so the compressed + write storage value is a lot higher. In the 2nd transaction, most of the wallet-specific data is already written, so we only need to store the new recipient.

The savings from packing the data are enough to offset the cost of storing all "long-term" words and addresses using contract storage (this can be seen in the first transaction, being cheaper even when writing storage).

The first transaction gives us a 15% gas cost reduction even when totally cold, subsequent transactions get a gas reduction of 47%.

The second transaction only needs to write to storage a single new recipient, so the difference between the two compression runs is a lot lower.

Send ETH uncompressed (1st): 0xa0efbb458309f1ccc14035a53e20c36155d722b1c5d991bfa7c43a21174ec468

Send ETH compressed + write storage (1st): 0x9a34d5787b0dd6fba248ebeb407d51526445b496f45f2b4f6ff1d56875f04f7c

Send ETH compressed (1st): 0x6197b0770cdb3efcdb252bf3932ff9964e3467906a7ac1de6361e2d9fe1bb84e

Send ETH uncompressed (2nd): 0x7b519df3f10a0e0ae507d6d18d775f1ed80e65c76df06e5632f402903cd9afb8

Send ETH compressed + write storage (2nd): 0x1680bae9b790bb54d522ebc033da92cb5261b73c27058767c55011957083ea41

Send ETH compressed + write storage (2nd): 0x1ccc93227065df0b9d6acc64504280ad7e55b5823b90111a0b6477c881291de4

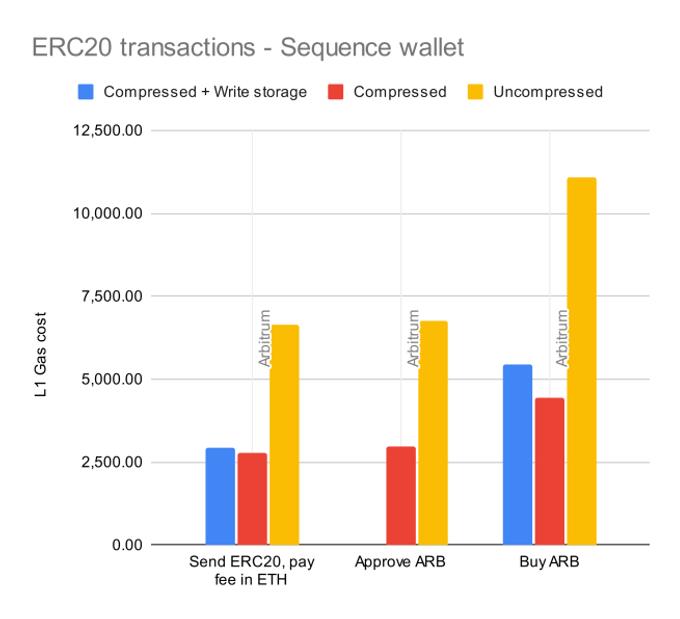
Send ERC20 Tokens

This is the example that we have seen so far. Testing both compressed, compressed (while writing storage), and uncompressed, we can see the following gas usage:

Transfering an ERC20 can be done for 50.60% less gas when we need to write the storage for the first time, and 54.24% when we have all the data in storage.

Approving is also a lot cheaper since we can represent the typical maximum approve value:

0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff

Using only 2 bytes. This gives us 52% savings when approving ERC20 transfers.

And since our compression algorithm is general purpose, we can compress more complex operations, like Uniswap swaps, giving us up to 56% savings on them.

Send ERC20 uncompressed: 0x0559ea8161e9cfed3298091d1f7626fe551bd40a38d2ff65d2340a52203e582a

Send ERC20 compressed + write storage: 0xbbf1d0250c37155f2da1d72cc01ff68fb5ccd4b4834a4accf53caf9374e64e3b

Send ERC20 compressed: 0x07e3b4de0b2cd3c8c531e90f32afc7a5dc3691b399ae4ab33d833b3e10741d05

Approve ERC20 uncompressed: 0x03c5f3d5c5a556439215c751a0d84b838266e9ec2481f862a912943e1bc309d6

Aprove ERC20 compressed: 0x7186dcf623d6bf5436691d28c649215900c4c71c2061863b0388786e07299428

Other Chains

Most EVM L1s tend to copy the gas cost model from Ethereum, but different L2s implement different models, affecting the compression performance.

Optimism

The Optimism-based rollups benefit similarly from the compression savings. This makes sense as both Arbitrum and Optimism publish their data in a similar fashion.

L1s - Ethereum, Polygon

Non-storage-based calldata saving schemas can be applied to L1s, but calldata is really cheap on them, so the "budget" left for decompression is too low. In short terms, with the current pricing schema of L1s, compression is not a viable strategy.

In the future, this may change if any of the ongoing proposals for increasing calldata cost on L1 take hold.

Next Steps

We are going to be rolling out our compression system on our L2 relayers. This will reduce most Sequence transactions to half of their original cost.

EIP-4844 is just around the corner. These gas optimizations, alongside the reduction of the calldata cost from using blobs, should compound together to make AA wallets an attractive option for L2s.

If you want to integrate this compression system into your contracts, you can find the libraries for encoding/decoding calldata, alongside a more detailed explanation of the inner workings of the system, all in this repository:

https://github.com/0xsequence/czip

We hope this post can inspire other smart contract wallets to implement these techniques. Making smart contract wallets more efficient will help alleviate the load of L2s while making Account Abstraction more attractive.